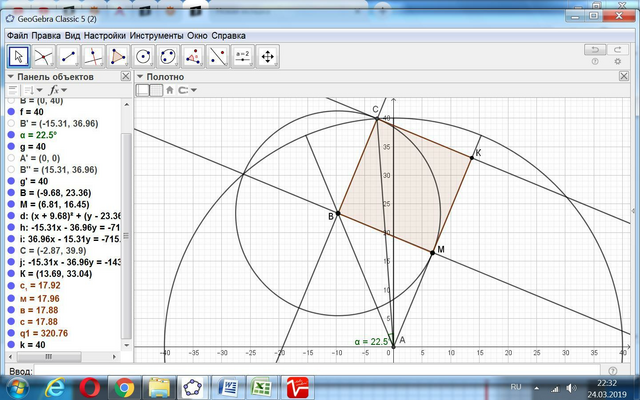
На стороне угла сектора возьмём точку В и проведём окружность радиусом R = х так, чтобы расстояния до второй стороны угла сектора и до дуги сектора были равны. Это получим стороны квадрата ВС и ВМ.
Вторая точка М пересечения принадлежит прямоугольному треугольнику МСА с катетами х и 2х.
По Пифагору х² + (2х)² = 40².
5х² = 1600,
х² = 1600/5 = 320 кв.ед.
Это и есть площадь квадрата.