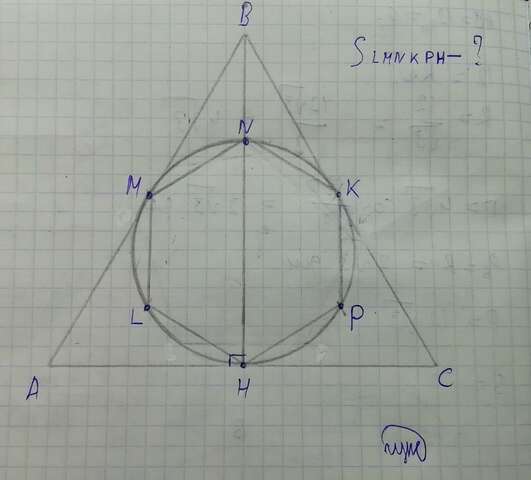
Построим высоту правильного треугольника BH, в который вписана окружность
AH = AC/2 (высота в правильном треугольнике является его медианой, т. е. делит сторону на две равные части)
Рассмотрим ΔABH - прямоугольный
AH = AC/2 = AB/2 (в правильном треугольнике все стороны равны)
По теореме Пифагора выразим катет BH

Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне

Найдем радиус описанной окружности около правильного треугольника, чтобы далее найти радиус вписанной. Для этого используем формулу:
a₃ = R√3, где a₃ - сторона правильного треугольника, R - радиус описанной окружности
Подставляем
12 = R√3

Найдем радиус вписанной окружности, используя формулу

где r - радиус вписанной окружности в правильный n-угольник, R - радиус описанной окружности около правильного n-угольника, n - число углов правильного треугольника (у нас правильный треугольник)
Подставляем

Радиус окружности, вписанной в правильный треугольник, является радиусом описанной окружности около правильного шестиугольника (R₂)
Формула для стороны правильного шестиугольника через радиус описанной около него окружности:
a₆ = R, где a₆ - сторона правильного шестиугольника, R - радиус описанной около него окружности
Подставив, получаем
a₆ = 2√3 дм
Найдем периметр правильного шестиугольника:
P = 2√3 * 6 = 12√3 дм
Найдем радиус вписанной окружности в правильный шестиугольник по той же формуле через радиус описанной окружности

Существует формула для нахождения площади правильного n-угольника:

где S - его площадь, P - его периметр, r - радиус вписанной в него окружности
Подставляем

Ответ: S = 18√3 дм²