Дано: f(x) = 7 - 8*x + 4*x²
М(1;4) - точка графика.
Найти: F(x)=?
Пошаговое объяснение: обратите внимание, что функция записана в обратном порядке степеней. Во-первых они имеют большее влияние, а во-вторых удобнее понять алгоритм интегрирования такой функции: степень увеличивается на единицу и такое же значение становится в знаменателе дроби.
Интегрируем - находим первообразную.

Теперь остаётся найти значение постоянной С по условию, что точка М принадлежит графику.
F(Mx) + C = My - условие задачи в общем виде. Находим значение С.
С = 4 - F(1) = 4 - (7*1 - 4*1² + 4/3*1³) = 4 - 4 1/3) = - 1/3 -постоянная.
F(x) = - 1/3 +7*x - 4*x² +4/3*x³ - первообразная - ответ.
·Дополнительно
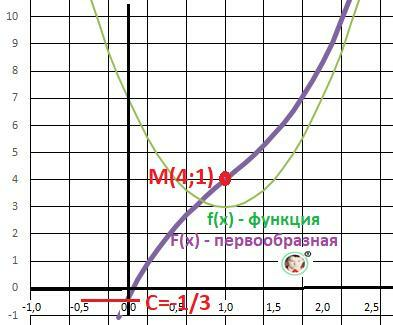
Рисунок с графиками функции и первообразной - расчёт подтверждается.