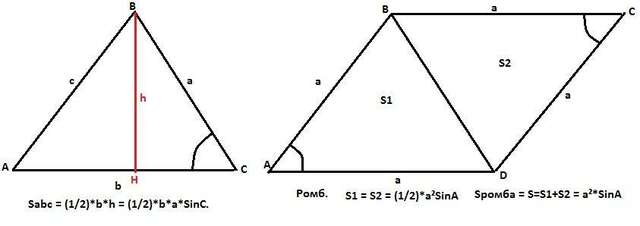
Для начала выведем формулу площади треугольника через две стороны и угол между ними. Известная нам формула площади:
Sabc = (1/2)*b*h (1), где b - сторона треугольника, а h - высота, проведенная у этой стороне. Рассмотрим прямоугольный треугольник СВН. В нем катет ВН - (высота h треугольника АВС, проведенная к стороне АС). В треугольнике СВН SinC = h/a (отношение противолежащего катета к гипотенузе). =>
h = a*SinC (2). Подставим (2) в (1):
Sabc = (1/2)*b*a*SinC. (3) То есть площадь ЛЮБОГО треугольника равна половине произведения двух его сторон на синус угла между ними.
Значит Sabc = (1/2)*a²*SinA.
В ромбе все стороны равны. Ромб делится диагональю на два равных треугольника. Противоположные углы ромба равны, а углы, прилежащие к одной стороне в сумме равны 180 градусов, то есть один угол α, а второй 180 - α. Sinα = Sin(180-α). Тогда площадь ромба равна из (3):
S=2*(1/2)*a*a*SinА = а²SinA, что и требовалось доказать.