Для графика квадратичной функций y=-x^2+6x-3 найдите 1)ось симметрий 2)промежуток... - Все ответы

87 просмотров

Для графика квадратичной функций y=-x^2+6x-3 найдите 1)ось симметрий 2)промежуток возрастания ,убывания 3)наибольшие значение функций 4)множество значений функций 5) Расстояние от вершины параболы до начальной координаты По возможности распишите пожалуйста

Алгебра Colddss_zn (162 баллов) 31 Май, 20 | 87 просмотров

Дан 1 ответ

Правильный ответ

$y=-x^2+6x-3$

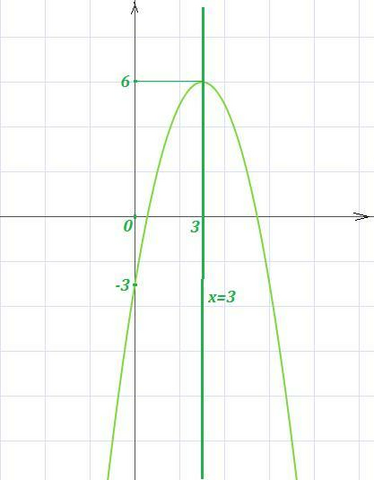
1) Ось симметрии проходит через вершину параболы, параллельно оси ОУ. Абсцисса вершины равна $x=-\frac{b}{2a}=-\frac{6}{-2}=3$ .

Уравнение оси симметрии: $x=3$ .

2) Так как ветви параболы направлены вниз (а=-1<0), то промежуток возрастания <img src="https://tex.z-dn.net/?f=%28-%5Cinfty%20%2C3%29" id="TexFormula4" title="(-\infty ,3)" alt="(-\infty ,3)" align="absmiddle" class="latex-formula"> , а промежуток убывания $(3,+\infty )$ .

3) Наибольшее значение функция принимает в своей вершине:

$y(3)=-3^2+6\cdot 3-3=-9+18-3=6$

4) Множество значений функции: $y\in (-\infty ,6\, ]$ .

5) Расстояние от вершины параболы до начала координат равно

$d=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}=\sqrt{(3-0)^2+(6-0)^2}=\sqrt{9+18}=\\\\=\sqrt{27}=\sqrt{9\cdot 3}=3\sqrt3$

NNNLLL54_zn (835k баллов) 31 Май, 20