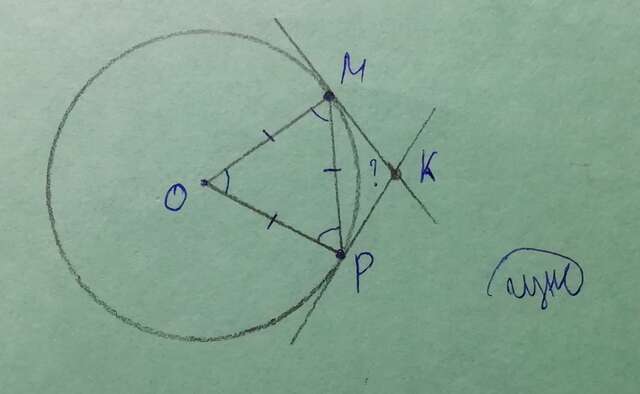
Проведем радиусы OM и OP, где M и P - точки касания касательных к окружности
Рассмотрим ΔOMP
OM = MP = OP ==> ΔOMP - равносторонний
В равностороннем треугольнике углы составляют по 60°
∠O = ∠M = ∠P = 60°
∠MPK = ∠OPK - ∠OPM = 90 - 60 = 30° (касательная к окружности перпендикулярна радиусу, проведенному в точку касания)
∠PKM = ∠OMK - ∠OMP = 90 - 60 = 30°
Рассмотрим ΔMKP: ∠M = ∠P = 30°, ∠MKP - ?
Угол между касательными есть ∠MKP
∠MKP = 180 - ∠M - ∠P = 180 - 30 - 30 = 120° (сумма углов треугольника составляет 180°)
Ответ: ∠MKP = 120°