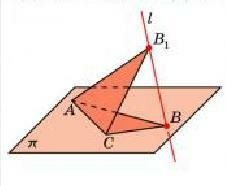
1) Параллельной проекцией равностороннего треугольника может быть треугольник произвольной формы.
Действительно, пусть дан произвольный треугольник ABC в плоскости π. Построим на одной из его сторон, например, AC равносторонний треугольник AB₁C так, чтобы точка B₁ не принадлежала плоскости π. Обозначим через l прямую, проходящую через точки B₁ и B. Тогда ясно, что треугольник ABC (произвольный) является параллельной проекцией равностороннего треугольника AB₁C на плоскость π в направлении прямой l. См. рисунок.
2) Найдём отношение  . Тогда по свойству параллельных проекций, если точка С делит заданный отрезок в отношении m:n , то проекция этой точки С₁ делит проекцию заданного отрезка в том же отношении. Следовательно,
. Тогда по свойству параллельных проекций, если точка С делит заданный отрезок в отношении m:n , то проекция этой точки С₁ делит проекцию заданного отрезка в том же отношении. Следовательно,  .
.