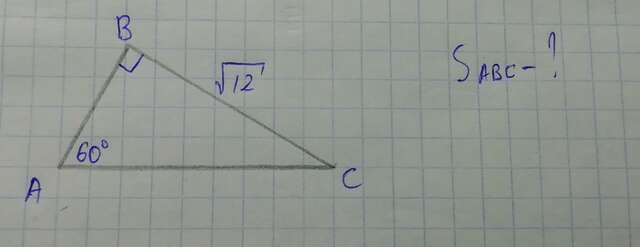
Синус угла в 60° равен √3/2 ==> sinA = √3/2
Синус угла прямоугольного треугольника - отношение противолежащего катета к гипотенузе

∠C = 90 - ∠A = 90 - 60 = 30° (сумма острых углов прямоугольного треугольника равна 90°)
AB = AC/2 = 4/2 = 2 (катет, лежащий напротив угла в 30°, равен половине гипотенузы)
Площадь прямоугольного треугольника равна половине произведения его катетов.

Ответ: S = √12