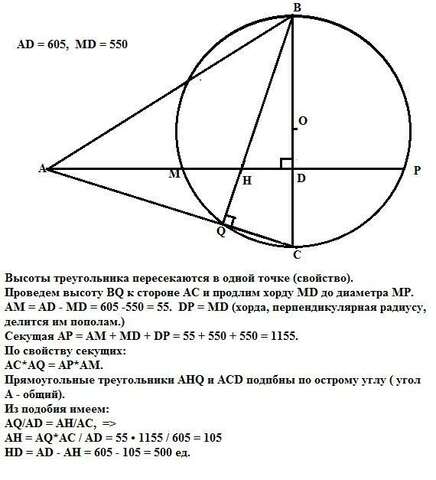
Высоты треугольника пересекаются в одной точке.
Проведем высоту BQ к стороне АС и продлим хорду MD до диаметра МР.
АМ = АD - MD = 605 -550 = 55. DР = MD (хорда, перпендикулярная радиусу, делится им пополам.)
Секущая AP = AM + MD + DP = 55 + 550 + 550 = 1155.
По свойству секущих:
АС*АQ = АР*АМ.
Прямоугольные треугольники АНQ и АСD подпбны по острому углу (угол А - общий).
Из подобия имеем:
АQ/АD = AH/AC => AH = AQ*AC / AD = 55 • 1155 / 605 = 105
HD = AD - AH = 605 - 105 = 500
Ответ: HD = 500 ед.