В прямоугольном треугольнике MNK, угол K=90°, KM=12, NK=12√3, KD-медиана. Найти угол KDN

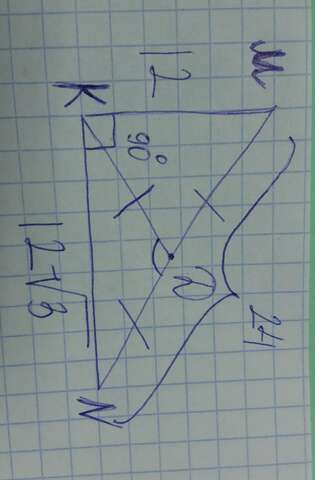
Медиана KD делит пополам сторону MN, т. е. MD=DN.

В прямоугольном треугольнике медиана, падающая на гипотенузу равна её половине=>KD=MD=DN.

По теореме Пифагора

$mn {}^{2} = mk {}^{2} + nk {}^{2} \\ mn = \sqrt{(12 \sqrt{3}) {}^{2} + 12 {}^{2} } = \sqrt{144 \times 3 + 144} = \sqrt{144(3 + 1) } = \sqrt{144 \times 4} = 12 \times 2 = 24$

Тогда KD=MD=DN=24/2=12

В треугольнике KMD KM=MD=DK=12=>он равносторонний.

В равностороннем треугольнике все углы равны 60°.

Тогда угол MDK=60°.

Углы MDK и NDK смежные=>угол NDK=180°-60°=120°.

Ответ:120