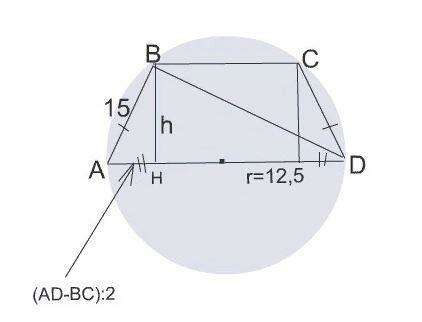
Дана трапеция АВСD, вокруг которой описана окружность.
АВ=СD=15 см
Площадь трапеции равна произведению ее высоты на полусумму оснований.
Известно только одно основание - оно равно диаметру окружности
АD=2 r=25 cм
Так как центр описанной окружности лежит на большем основании трапеции,
диаметр окружности, ее боковая сторона и диагональ образуют прямоугольный треугольник с гипотенузой, равной диаметру.
Высоту трапеции h = ВD найдем по формуле высоты прямоугольного треугольника, проведенного из прямого угла к гипотенузе:
h = 2s/a , где а - гипотенуза.
Площадь треугольника пока не известна.
Для ее нахождения нужно найти длину второго катета -диагонали трапеции ВD.
ВD=√(АD²-АВ²)=√(25²-15²)=√400=20 см
2s ABD=АВ·ВD=15·20=300 cм²
h =300:25= 12 см
Отрезок от А до основания Н высоты ВН трапеции равен в равнобедренной трапеции полуразности оснований.
АН найдем из прямоугольного треугольника АВН по теореме Пифагора.
Полуразность оснований 9 см
Разность оснований 18 см
Меньшее основание
ВС= 25 -18=7 см
S трапеции = 12·(25+7):2 =192 см²