1.
Дано: Δ АВС, S=9√3 cм², АВ=12 см, АС=3 см. Найти ∠ВАС.
Решение: угол ВАС найдем из формулы площади треугольника S=1\2a*b*sinα
9√3=1\2 * 12 * 3 * sinВАС
18sinВАС=9√3, sinВАС=√3\2, ∠ВАС=60°.
Ответ: 60°.
2.
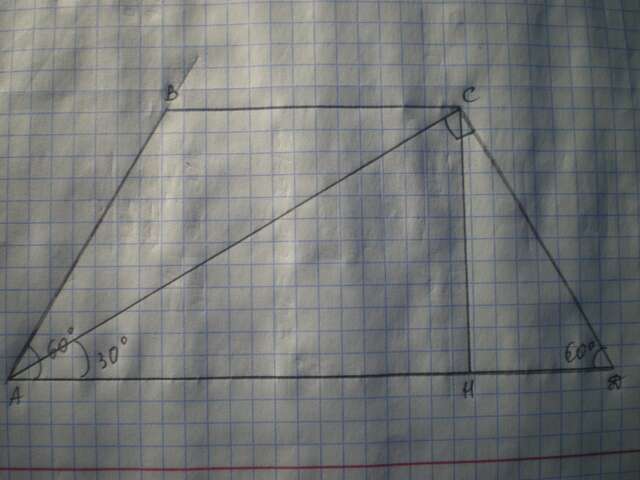
Дано: АВСД - трапеция, АВ=СД, АД=20√3, ∠А=∠Д=60°, АС⊥СД. Найти S(АВСД).
Решение: Проведем высоту СН, тогда S(АВСД)=(ВС+АД):2*СН.
Рассмотрим ΔАСД - прямоугольный, ∠Д=60°, тогда ∠САД=90-60=30°, а СД=1\2 АД=20√3:2=10√3.
Диагональ АС перпендикулярна к боковой стороне и делит угол А пополам, значит большее основание трапеции в два раза больше меньшего основания и её боковых сторон; и высота трапеции равна половине её диагонали.
СД=ВС=20√3:2=10√3;
АС²=(20√3)²-(10√3)²=1200-300=900; АС=√900=30.
СН=1\2 АС=30:2=15.
S(АВСД)=(20√3+10√3):2*15=225√3 (ед²).
Ответ: 225√3 ед²