ABC, ABC1 - равнобедренные и прямоугольные треугольники. AB=12см, альфа перпендикулярна...

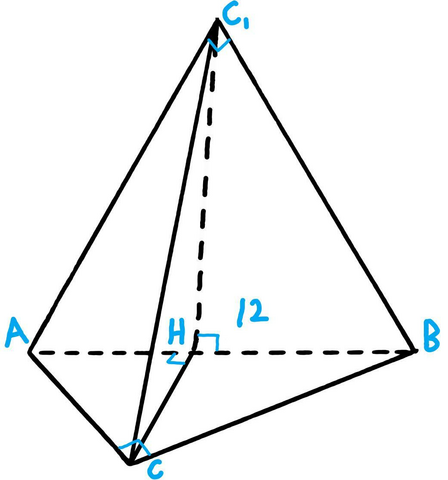
Пусть ABC ⊂ α, а ABC₁ ⊂ β

Две плоскости будут перпендикулярны когда угол между этими плоскостями будет равен 90°

Опустим высоты из вершин C и C₁ на сторону AB. Они пересекутся в точке H.

Следовательно угол между α и β = ∠C₁HC = 90°

Рассмотрим ΔABC

Гипотенуза этого треугольника равна

$AB = \sqrt2\cdot AC$

Следовательно

$AC = \dfrac{AB}{\sqrt2}\\\\\\AC = \dfrac{12}{\sqrt2} = 6\sqrt2 cm$

Так как треугольник равнобедренный, то CB = AC = 6√2 см

Найдём площадь треугольника S

$S = \dfrac{1}{2}AC\cdot BC = \dfrac{1}{2} \cdot6\sqrt2\cdot6\sqrt2 = 36 \;\;cm^2$

Найдём CH

$S = \frac{1}{2}\cdot AB\cdot CH \Rightarrow CH = \dfrac{2S}{AB}\\\\CH = \dfrac{72}{12} = 6 \;\;cm$

Так как ΔABC₁ - равнобедренный и имеет общую гипотенузу с ΔABC, то ΔABC₁ = ΔABC

ΔABC₁ = ΔABC ⇒ C₁H = CH = 6 см.

Рассмотрим ΔHCC₁

CH = C₁H и ∠C₁HC = 90 ⇒ ΔHCC₁ - прямоугольный, равнобедренный

CC₁ = √2 CH = 6√2 см.