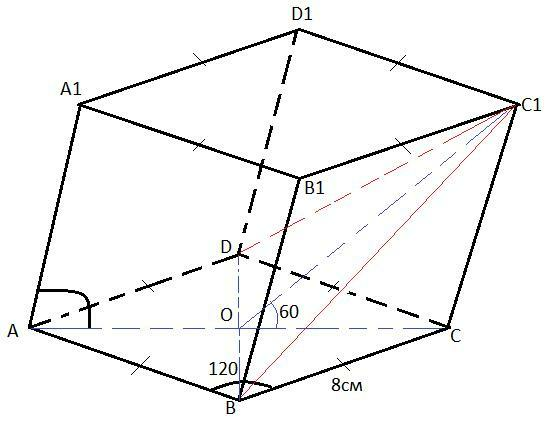
AA1⊥(ABC) это условие. Диагонали ромба пересекаются под прямым углом и делятся точкой пересечения пополам. BO=OD. Значит CO и C1O высоты треугольников DCB и DBC1 соответственно, высоты они потому, что треугольники равнобедренные(мы работаем в призме и основание ромб), а значит медианы это и высоты. Из условия и определения угла между плоскостью угол между этими прямыми 60°. Чтобы найти площадь призмы надо площадь основания умножить на ребро призмы, найдём это ребро, посчитаем всё остальное.

Ответ: 384√3 см³.