Пошаговое объяснение:
Для этого надо найти корни первой производной функции.
А) Дано: y(x) = 16*x³ + 12*x² - 5.
y'(x) = 16*3*x² + 12*2*x = 48*x² - 24*x = 48*x*(x - 1/2) = 0.
Нули производной: х1 = 0 и х2 - 0,5.
Локальные экстремумы.
7. Локальные экстремумы.
Максимум Ymax(-0,5) =-4. Минимум Ymin(0) =-5
8. Интервалы возрастания и убывания.
Возрастает Х∈(-∞;-0,5;]U[0;+∞) , убывает - Х∈[-0,5;0]
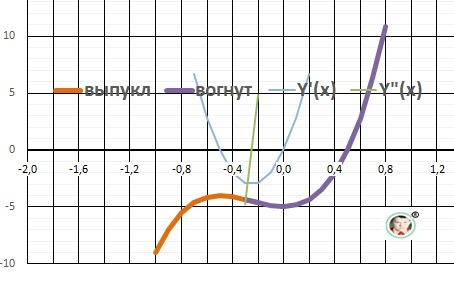
График функции на рисунке в приложении.
Б) Дано: y(x) = x + 16/x
y'(x) = 1 - 16/x² = (x-4)*(x+4)/x² = 0
x1 = - 4, x2 = 4.
При Х=0 - разрыв функции.
Возрастает: X∈(-∞;-4]∪[4;+∞). Убывает: X∈[-4;0)∪(0;4]