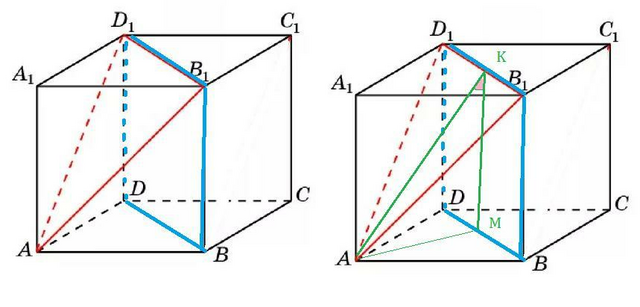
Пусть ребро куба равно 1.
Тогда диагонали квадратов со стороной 1 равны √(1²+1²)=√2
AB₁=AD=В₁D₁=√2
Плоскости АВ₁D₁ и BDB₁ пересекаются по прямой В₁D₁ .
Осталось провести высоту АК равностороннего треугольника АВ₁D₁
и КM || BB₁
Из прямоугольного треугольника АКМ
cos∠AKM=KM/AK
АК - высота равностороннего треугольника АВ₁D₁
АК=AB₁·sin60°=√2·(√3/2)=(√6)/2
cos∠AKM=(√6)/2
∠AKM=arccos((√6)/2)