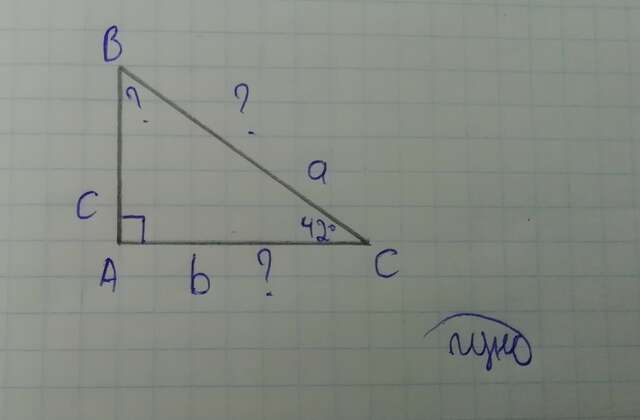
∠B = 90 - 42 = 48° (сумма острых углов прямоугольного треугольника равна 90°)
Найдем гипотенузу, используя теорему синусов

По теореме Пифагора
a² = b² + c²
18² = b² + 12²
324 = b² + 144
b² = 324 - 144 = 180
b = √180 ≈ 13,4 см
Ответ: ∠B = 48°, a ≈ 18 см, b ≈ 13,4 см