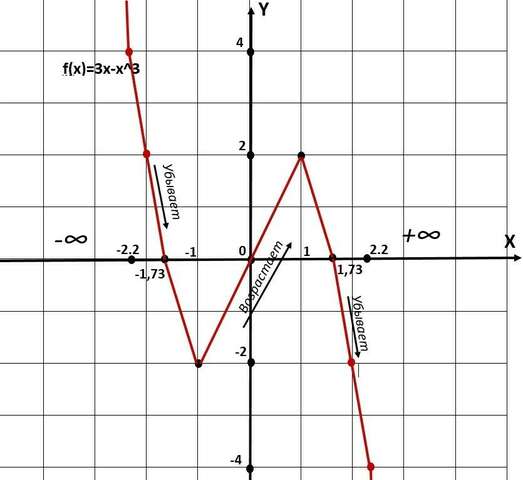
F(x)=3x-x^3
1. Найдём точки пересечения с осью оХ
3x-x^3=0
x(3-x^2)=0
x=0
3-x^2=0
x^2=3
x= √3 ≈ 1,73
x=-√3 ≈ -1,73
2. Найдём точки экстремума
f'(x)=0
f'(x)=(3x-x^3)'=3-3х^2
3-3х^2=0
х^2=1
х= 1 f(1)=3*1-1^3=3-1=2
х=-1 f(-1)=3*(-1)-(-1)^3=-3+1=-2
3. Определим убывание и возрастания f(x)
Если f '(x)‹0 то f(x) убывает
Если f '(x)›0 то f(x) возрастает
интервалы убывания-возрастания
(-∞;-1) f '(x)‹0 f(x) убывает
(-1; 1) f '(x)›0 f(x) возрастает
( 1; ∞) f '(x)‹0 f(x) убывает
Строим график см ниже
f(2) =3*2-2^3=6-8=2
f(-2)=3*(-2)-(-2)^3=-6+8=-2
f(2.2) =-4
f(-2.2)= 4