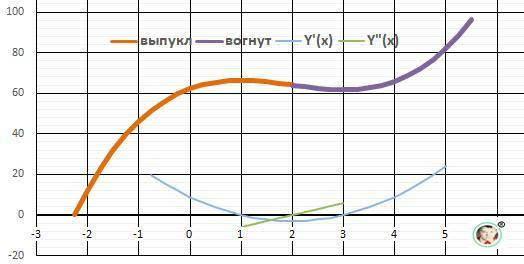
ДАНО:Y(x) = x³ - 6*x² + 9*x +62
Найти: Локальные экстремумы.
1. Первая производная. Y'(x) = 3*x² -12*x + 9 = 0 - решаем квадратное уравнение.
Корни Y'(x)=0. Х = 1 Х= 3.
2. Локальные экстремумы.
Максимум - Ymax(1) = 1-6+9+62 = 66 - ответ.
Дополнительно.
Минимум - Ymin(3) =62
3. Интервалы возрастания и убывания.
Возрастает Х∈(-∞;1;]U[3;+∞) , убывает - Х∈[1;3]
4. График в приложении.