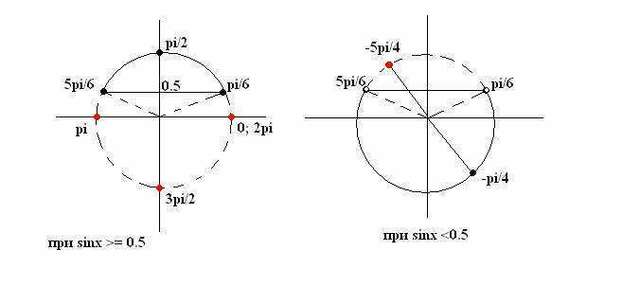
1) sinx - 1/2 >=0
sinx>=1/2
pi/6 + 2pi*k <=x<=5pi/6 + 2pi*k<br>sinx - 0.5 = cosx + 0.5
sinx - cosx = 1
cosx = sqrt(1 - sin^2(x))
sinx - sqrt(1 - sin^2(x)) = 1
sqrt(1 - sin^2(x)) = sinx - 1 -возведем в квадрат обе части
1 - sin^2(x) = sin^2(x) - 2sinx + 1
2sin^2(x) - 2sinx = 0
sinx*(sinx - 1) = 0
sinx = 0, x = pi*k - не входит в интервал pi/6 + 2pi*k <=x<=5pi/6 + 2pi*k<br>sinx = 1, x = pi/2 + pi*k - входит в интервал только одна точка, а именно:
x=pi/2 + 2pi*k
2) sinx - 1/2 < 0
sinx < 0.5
5pi/6 + 2pi*k < x < 13pi/6 + 2pi*k
0.5 - sinx = cosx + 0.5
-sinx = cosx - разделим все на (- cosx)
tgx = -1
x = - pi/4 + pi*k - входит в решение только x= -pi/4 + 2pi*k
Ответ: x = pi/2 + 2pi*k, x = -pi/4 + 2pi*k
P.S. Для большего понимания выбора корней смотрите рисунок