Площадь трапеции находится по формуле

где a, b -- основания трапеции, h -- высота.
h = 10 см, S = 240 см² по условию
Пусть меньшее основание равно x см, тогда большее равно (x + 4) см.
Составим уравнение, используя формулу площади трапеции:

Таким образом, меньшее основание BC равно 22 см, а большее AD равно (22+4) = 26 см.
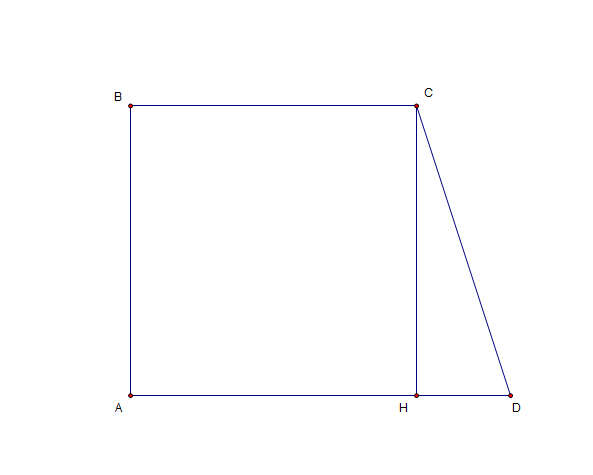
В прямоугольной трапеции одна из боковых сторон равна высоте, то есть AB = 10 см.
Проведём из точки С высоту CH. Тогда HD = AD - BC = 26 - 22 = 4 см
CH = h = 10 см. По теореме Пифагора найдём CD:

Ответ: 10 см, 22 см, 26 см, 2√29 см