Ответ:
28 см
Пошаговое объяснение:
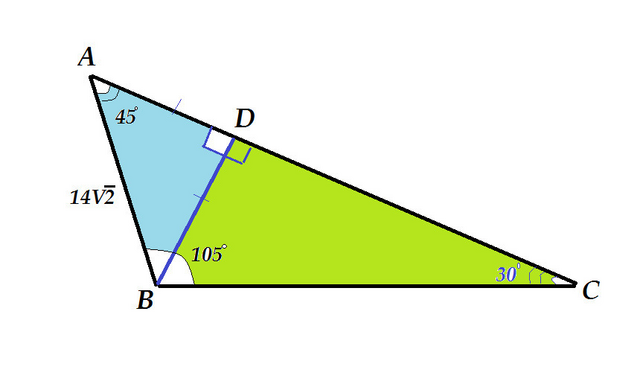
Дано: Δ АВС
∠А = 45°
∠В = 105°
меньш. стор. =14√2 см
Найти: средн. стор.
Решение.
Рассмотрим ΔАВС. ∠С = 180° - ∠А - ∠В = 180° - 45° - 105° = 30°
30° < 45° < 105°, т.е. ∠С < ∠A < ∠В
Так как против меньшего угла лежит меньшая сторона, то это сторона АВ, лежащая против ∠ С, а средней стороной будет ВС, лежащая против ∠А.
Опустим из ∠В высоту ВD к стороне АС.
Рассмотрим ΔABD. ∠АDВ = 90° по построению, ∠А = 45° по условию, ⇒ ∠АВD = 90° - 45° = 45°, т.е. ΔАВD - равнобедренный прямоугольный, где АВ - гипотенуза, а АD и ВD - катеты.
По теореме Пифагора ВD = AD = √(АВ²/2) = √(2*14²/2) = 14 (см)
Рассмотрим Δ ВСD. Он прямоугольный, т.к. ВD высота к стороне АС и ВС - гипотенуза этого треугольника. ∠С = 30°, а ВD - катет, лежащий против угла 30°, он равен половине гипотенузы. ⇒
ВС = 2ВD = 2*14 = 28 (cм)
Ответ: 28 см