Раскрываем моули по определению т.к. переменная не только под модулем, но и за ним.
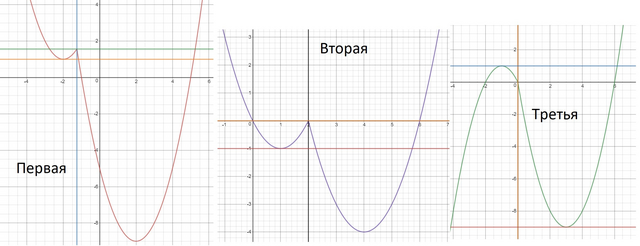
Первая.


Для первого уравнения: координаты вершины (2;-9), парабола направлена вверх, точки пересечения с осями: 
Для второго уравнения: координаты вершины (-2;1), парабола направлена вверх, точки пересечения с осями:  .
.
Дальше мы рисуем отдельно два этих графика проводим прямую x= -1.25 И для каждого графика смотрим что будет когда х меньше или больше этой прямой, так же необходимо проверить сходятся ли графики в точке (-1,25;y).

Да всё сходится можем строить график этой функции.
Смотря на график можно увидеть, когда прямая y=m имеет с графиков всего 3 общие точки, когда прямая касается вершины левой параболы или когда прямая касается точки пересечения двух парабол.
Ответ: m={1;25/16}.
Вторая.


Для первого уравнения: парабола вверх, координаты вершины (4;-4), точки пересечения с осями: 
Для второго уравнения: парабола вверх, координаты вершины (1;-1), точки пересечения с осями: 
Дальше мы отдельно рисуем два графика проводим на них прямую x=2 и видим что меньше или больше этой точки. Проверяем сходятся ли эти графики в точке (2;y).

Да сходятся, можем стоить общий график.
Прямая y=m имеет с графиком 3 общие точки, когда касается вершины левой параболы или касается их точки пересечения.
Ответ: m={-1;0}.
Третья.


Для первого уравнения: парабола вверх, координаты вершины (3;-9), точки пересечения с осями: 
Для второго уравнения: парабола вниз, координаты вершины (-1;1), точки пересечения с осями: 
Строим отдельно и смотрим, что меньше или больше относительно прямой x=0, графики сходятся в точке (0;0) т.к.

Строим общий график на одной координатной плоскости и видим, что прямая y=m имеет с графиком две общие точки, когда она касается вершины левой параболы или правой параболы.
Ответ: m={-9;1}.