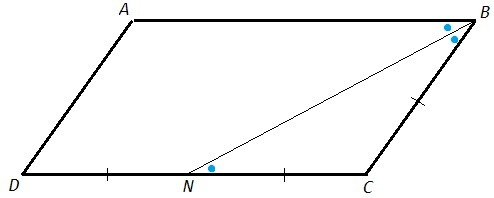
1) CN=CD/2=BC => △BCN - равнобедренный, углы при основании равны, ∠CBN=∠CNB
∠ABN=∠CNB (накрест лежащие при AB||CD)
∠ABN=∠CBN, BN - биссектриса ∠ABC (делит угол на два равных)
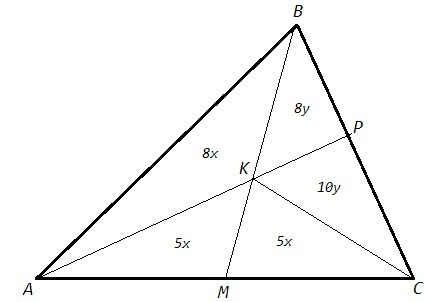
2) Площади треугольников с равной высотой относятся как их основания. Обозначим площади ABK=8x, AKM=MKC=5x, ACK=10x. Площади треугольников с равным основанием относятся как их высоты. Высоты треугольников ABK и ACK относятся как 8:10. Следовательно площади BKP и CKP относятся как 8:10. Обозначим площади BKP=8y, BKC=18y. Площади BKC и MKC относятся как 8:5.
S(BKC)/S(MKC) =18y/5x =8/5
S(BKP)/S(AKM) =8y/5x =8/5 * 4/9 =32/45
Или по теореме Менелая:
CP/PB *BK/KM *MA/AC =1 <=> CP/PB *8/5 *1/2 =1 <=> CP/PB=10/8
CM/MA *AK/KP *PB/BC =1 <=> AK/KP *8/18 =1 <=> AK/KP=18/8
Площади треугольников с равным углом относятся как произведения сторон, заключающих равные углы.
S(BKP)/S(AKM) =BK*KP/AK*KM =8/5 *8/18 =32/45