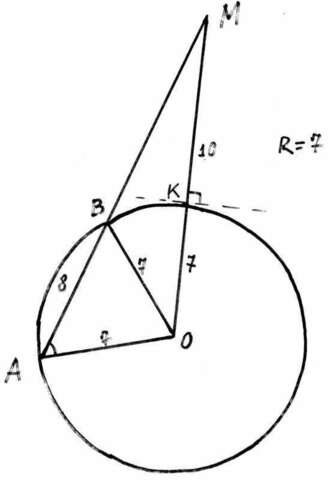
Кратчайшее расстояние от точки М до окружности -перпендикуляр к касательной, проходящий через центр окружности О. По условию ОМ=17, ОК=10, тогда радиус окружности R=17-10=7. Проведём радиусы(смотри рисунок), к точкам А и В. По теореме косинусов найдём в треугольнике АОВ косинус угла А. ВОквадрат=АОквадрат+АВквадрат-2*АО*АВ*cosA. 49=49+64+2*7*8*cosA. Отсюда cosA=0,57. Также в треугольнике АОМ. ОМквадрат=АОквадрат+ АМквадрат-2*АО*АМ*cosA. 289=49 +АМквадрат-2*7*АМ*0,57. Пусть АМ=Х, тогда Хквадрат-8Х-240=0. Решая квадратное уравнение получим Х=20, то есть искомые расстояния АМ=20, ВМ=20-8=12.