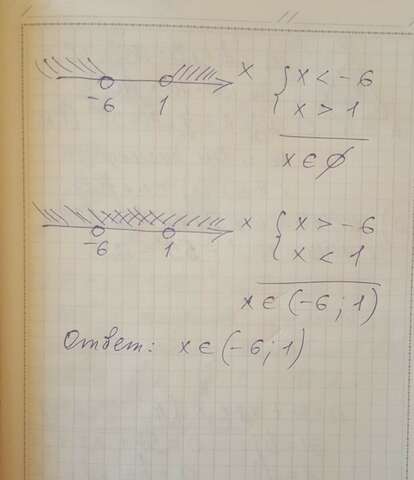Знайти суму цілих розв'язків нерівності (2x+3)^2-(x+2)(x-5)

${(2x + 3)}^{2} - (x + 2)(x - 5) < 37 \\ 4 {x}^{2} + 12x + 9 - {x}^{2} + 5x - 2x + 10 - 37 < 0 \\ 3 {x}^{2} + 15x - 18 < 0 \: \: \: \: \: | \div 3 \\ {x}^{2} + 5x - 6 < 0 \\ по \: теореме \: Виетта \: \\ x1 = - 6 \: \: \: \: x2 = 1$

0\\ x - 1 > 0 \: \: \: \: \: \: x - 1 < 0 \\ x < - 6 \: \: \: \: \: \: \: \: \: \: x > - 6\\ x > 1 \: \: \: \: \: \: \: \: \: \: \: \: \: x < 1 " alt="разложим \: на \: множители: \\ (x - x1)(x - x2) < 0 \\ (x + 6)(x - 1) < 0 \\- - - - - - \\ x + 6 < 0 \: \: \: \: \: \: x + 6 > 0\\ x - 1 > 0 \: \: \: \: \: \: x - 1 < 0 \\ x < - 6 \: \: \: \: \: \: \: \: \: \: x > - 6\\ x > 1 \: \: \: \: \: \: \: \: \: \: \: \: \: x < 1 " align="absmiddle" class="latex-formula">

ответ с рисунком на фото