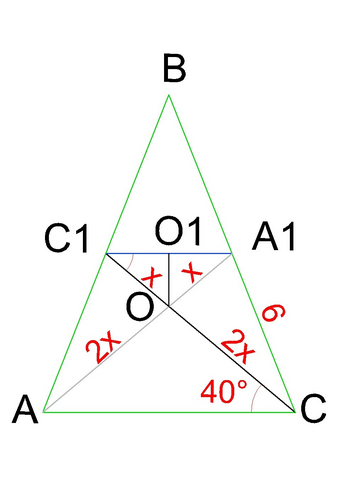
Проведем С₁А₁. С₁А₁║АС, так как АС₁=СА₁, ∠ВАС=∠АСВ (треугольник равнобедренный). Из параллельности С₁А₁║АС, следует, что СС₁ как секущая образует равные углы ∠АСС₁ = ∠СС₁А₁=40° (накрест лежащие углы).
Медианы равнобедренного треугольника точкой пересечения делятся на отрезки, соотношение длин которых 2:1, а так как АА₁=СС₁, то и отрезки ОС₁=ОА₁ и СО=АО. Обозначим стороны ОС₁=ОА₁ за х, тогда СО=АО=2х, а искомая медиана СС₁=3х.
Из точки О опустим высоту ОО₁ на С₁А₁. ОО₁ также является медианой ΔОС₁А₁, . Найдем С₁О₁ как катет прямоугольного ΔОС₁О₁.
С₁О₁=х·cosOC₁O₁=x·cos40°.
С₁А₁=2·С₁О₁=2x·cos40°.
По теореме косинусов из ΔСС₁А₁ найдем х.
6²=(2x·cos40°)²+9х²-2·3х·2x·cos40°·cos40°
36=х²·(9-8·cos²40°)
х=6/√(9-8·cos²40°)
СС₁=3х=18/√(9-8·cos²40°)≈8,67 см
Ответ: СС₁=18/√(9-8·cos²40°)
(задача проверена графическим методом. всё совпало)