Площадь треугольника равна половине произведения высоты на длину стороны, к которой проведена. S=h•a/2. Основания ∆ АВМ и ∆ СВМ равны, высота из вершины В – общая. ⇒
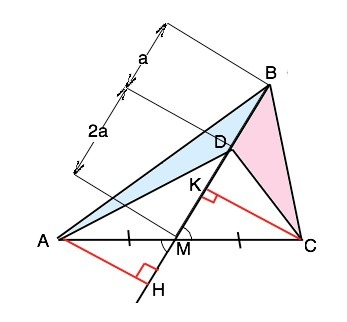
Медиана треугольника делит его на два равновеликих ( равных по площади) треугольника, S(АВМ)=S(CBM)=72:2=36 см² Продолжим медиану ВМ и проведем к ней из А и С высоту АН треугольника АВD и высоту СК –∆ СВD. Прямоугольные ∆ АМН=∆ КСМ по гипотенузе и острому углу при М ( вертикальные). Следовательно, АН=СК. Основание ВD у этих треугольников общее, высоты равны, поэтому АВD и CBD равновелики. В ∆ АВD и ∆ АВМ высота АН общая, а основания относятся как BD:ВM=1/3.
Площади треугольников с равными высотами относятся как длины их оснований. ⇒ S(ABD)=S(CBD)=S(ABM)•1/3=12 см²