№8.



Сложим эти уравнения:


3x 3x-2*3=0" alt="y=3;=>3x-2*3=0" align="absmiddle" class="latex-formula">
3x-2*3=0" alt="y=3;=>3x-2*3=0" align="absmiddle" class="latex-formula">


Находим произведение:

Ответ под цифрой 2) 6
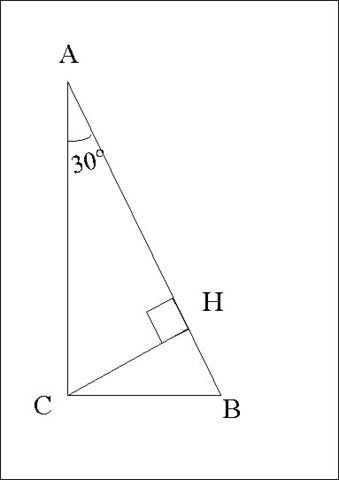
№9
1) В прямоугольном треугольнике катет, лежащий против угла в 30°, равен половине гипотенузы.
По условию гипотенуза АВ = 90√3, значит, катет СВ, лежащий против угла в 30°, равен половине гипотенузы.
СВ=90√3:2=45√3
2) По теореме Пифагора находим второй катет
АС² = АВ²-СВ²
АС²=(90√3)²-(45√3)²
АС²=135²
АC=135
3) СН - высота, значит, Δ АСН - прямоугольный.
В прямоугольном треугольнике катет, лежащий против угла в 30°, равен половине гипотенузы.
Гипотенуза АС = 135, значит, катет СН, лежащий против угла в 30°, равен половине гипотенузы.
СН=135:2=67,5 см
Ответ: 67,5 см