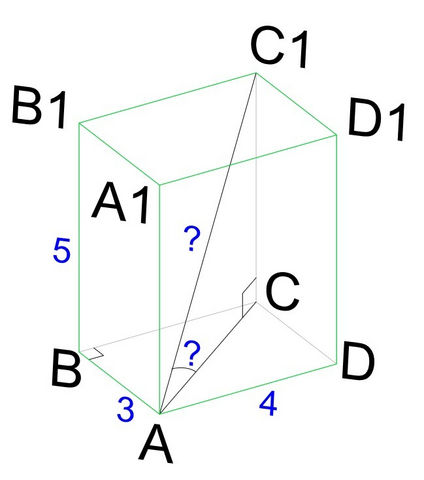
1. Рассмотрим рисунок.
Найдем диагональ АС основания АВСD которая является гипотенузой в ΔADC: АС=√(AD²+AB²)=√(16+9)=5 см
а) Из прямоугольного треугольника АСС₁, образованного диагональю параллелепипеда, найдем гипотенузу АС₁=√(АС²+СС₁²)=√(25+25)=√50=5√2 см
б) Расстояние от прямой АВ до прямой В₁С₁ равно высоте параллелепипеда ВВ₁=5 см (АВ и В₁С₁ - скрещивающиеся, и кратчайшее расстояние между ними равно ВВ₁ )
в) Прямоугольный ΔАСС₁ - равнобедренный, т.к. АС=СС₁=5 см, поэтому ∠САС₁= =45°
=45°
∠САС₁ - является углом между диагональю параллелепипеда и плоскостью основания. sin ∠САС₁= sin45°=√2/2
г) S=2*(4*3+4*5+3*5)=94 см²
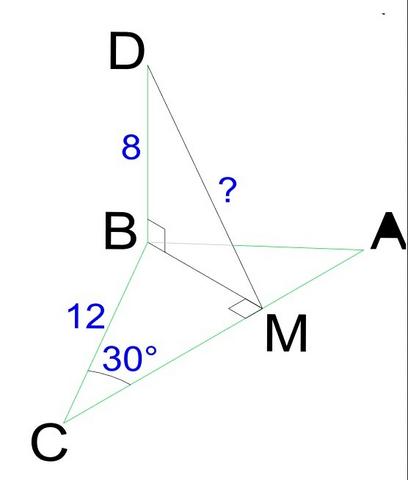
2. Рассмотрим рисунок.
Из прямоугольного ΔВСМ найдем ВМ=СВ·sin∠BCM=12·sin30°=6.
Из прямоугольного ΔDMB найдем DM=√(BD²+BM²)=√(64+36)=10
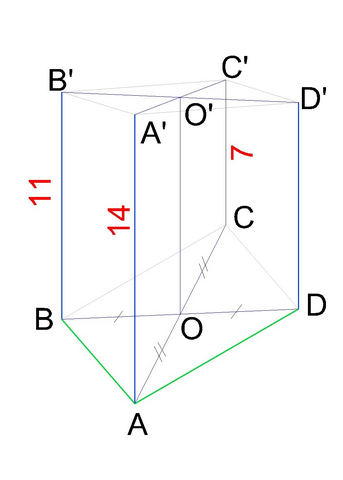
3. Для решения задачи построим диагонали параллелограмма. Они пересекаются в точке О, которая делит их пополам.
Построим высоты АА’=14 см, ВВ’=11 см, СС’= 7 см и ОО’. Образовалась прямоугольная трапеция АА’С’С со средней линией ОО’. ОО’ является также расстоянием от плоскости α до точки О. Найдем ОО’=(АА’+СС’)/2=10,5 см.
Очевидно, что если провести высоту DD’ от плоскости α в точку D, то получится прямоугольная трапеция ВВ’ D’D, в которой ОО’ является средней линией, а DD’ - меньшим основанием. Найдем DD’=х.
10,5 = (11+х)/2
х=10
Ответ: вершина D удалена от плоскости α на 10 см.