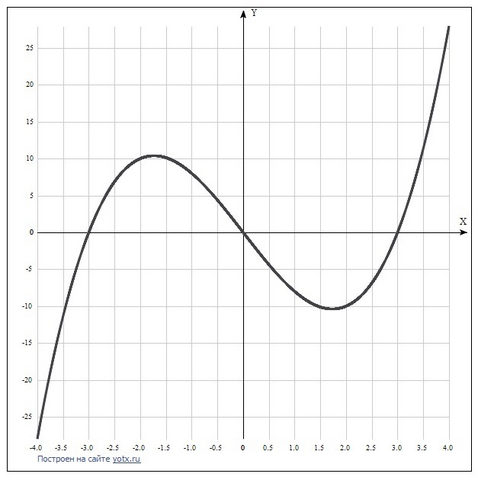
Дана функция y = х³- 9x.
1) Область определения х ∈ (-∞, +∞).
2) Разложим её на множители: у = х(х - 3)(х + 3).
Отсюда получаем 3 точки пересечения оси Ох:
х1 = 0, х2 = 3, х3 = -3.
3) Точка пересечения оси Оу: х = 0.
4) Поведение на бесконечности.
У(-∞) = -∞
У(+∞) = +∞
5) Исследование на четность.
Y(-х) = - х³ + 9х = -(х³ - 9х).
Функция нечетная.
6) Монотонность.
Производная функции
Y' = 3x²- 9 = 3(х² - 3).
Точки экстремумов
х1 = √3 х2 = -√3.
Находим знаки производной на полученных промежутках.
х = -2 -√3 0 √3 2
y' = 3 0 -9 0 3.
В точке х = -√3 максимум, у = 6√3,
в точке х = √3 минимум, у = -6√3.
Возрастает на промежутках (-∞, -√3) ∪ (√3, +∞)
Убывает на промежутке (-√3, √3).
7) Точки перегиба - нули второй производной.
Y" = 6x = 0
Х= 0. Это точка перегиба.
Выпуклая: х ∈ (-∞; 0]
Вогнутая: х ∈ (0; +∞).