Две стороны треугольника abc равны 5 и 8 см, угол между ними 120 градусов, найдите третью...

Question

Две стороны треугольника abc равны 5 и 8 см, угол между ними 120 градусов, найдите третью сторону Срочно

Answer 1

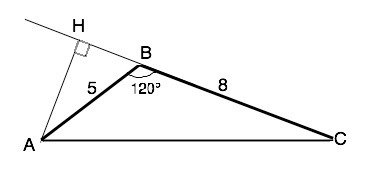
 Вариант решения. Пусть данный треугольник АВС, АВ=5, ВС=8, угол АВС=120°.  АН - высота из острого угла (в тупоугольном треугольнике  лежит вне его). Угол АВН=60°, как смежный углу 120°. Тогда АН=AB•sin60°=5•(√3/2)=2,5√3 см,    BH=AB•cos60°=5•1/2=2,5 см. Отсюда СН=ВН+ВС=10,5 см. По т.Пифагора АС=√(AH²+CH²)=√[(2√3)²+(10,5)²]= √129 см.

---

Answer 2

теорема косинусов

x - третья сторона

x^2 = 5^2 +8^2 -2*5*8*cos120 = 25+64-80*(-0,5) = 25+64+40 = 129

x = √ 129 см

Comments

три стороны треугольникаa = 5 см; b = 8 см; с = ?угол между a и b 120 градформула косинусовc^2 = a^2 +b^2 - 2 a b cos(120) ^2 во второй степениc^2 = 5^2 +8^2 - 2 *5 *8 * (-1/2) = 25 +64 +40 = 129c = √129 смответтретья сторона √129 см