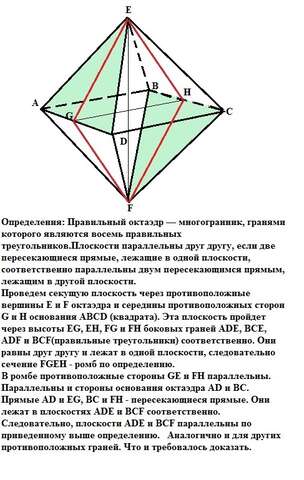
Определения: Правильный октаэдр — многогранник, гранями которого являются восемь правильных треугольников.
Плоскости параллельны друг другу, если две пересекающиеся прямые, лежащие в одной плоскости, соответственно параллельны двум пересекающимся прямым, лежащим в другой плоскости.
Проведем секущую плоскость через противоположные вершины Е и F октаэдра и середины противоположных сторон G и H основания АВСD (квадрата). Эта плоскость пройдет через высоты EG, EH, FG и FH боковых граней ADE, BCE, ADF и BCF(правильные треугольники) соответственно. Они равны друг другу и лежат в одной плоскости, следовательно сечение FGEH - ромб по определению.
В ромбе противоположные стороны GE и FH параллельны. Параллельны и стороны основания октаэдра AD и ВС. Прямые AD и EG, BC и FH - пересекающиеся прямые. Они лежат в плоскостях ADE и BCF соответственно. Следовательно, плоскости ADE и BCF параллельны по приведенному выше определению. Аналогично и для других противоположных граней. Что и требовалось доказать.