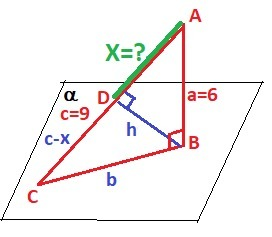
Дано:
Плоскость α, точка А∉α.
АВ = 6 см - перпендикуляр к пл. α
АС = 9 см - наклонная
Найти: AD=? - проекцию АВ на АС.
Решение:
Рисунок к задаче в приложении.
BD ⊥AC - перпендикуляр к АС.
BC = b - катет ΔАВС, AD = h - катет двух треугольников - ΔABD и ΔBCD. Применяем теорему Пифагора.
b² = c² - a² - запомнили.
Катет h общий и можно написать равенство:
a² - x² = b² - (c -x)² - раскрываем скобки.
a² - x² = b² - c² + 2*c*x - x² - упрощаем.
2*с*x = a² - b² + c² - подставим значение b².
2*c*x = a² - c² + a² + c² = 2*a² - упрощаем и находим неизвестное Х.
x = a²/c = 6²/9 = 36 :9 = 4 см - проекция AD - ОТВЕТ
Проверка - вычислим катет h.
h = √(6²-4²) = √20 = 4√5 - из ΔABD.
b² = 9² - 6² = 81 - 36 = 45
c - x = 9 - 4 = 5
h = √(45-25) = √20 = 4√5 - из ΔBCD.
Результат одинаковый. Расчёт правильный.