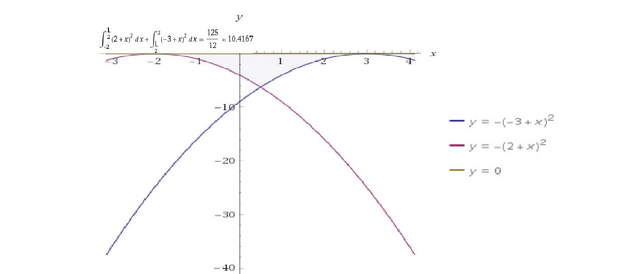
Даны уравнения парабол: у = -х² + 6х - 9 и у = -х² - 4х - 4.
Если их преобразовать, выделив полные квадраты, то получим:
у = -(х - 3)² и у = -(х + 2)².
Точки х = -2 и х = 3 при у = 0 это координаты вершин парабол.
Найдём точку пересечения парабол:
-х² + 6х - 9 = -х² - 4х - 4.
10х = 5,
х = 5/10 = 1/2.
Отсюда искомая площадь разбивается на 2 участка: (-2; (1/2)) и ((1/2); 3).
Площадь равна сумме интегралов: