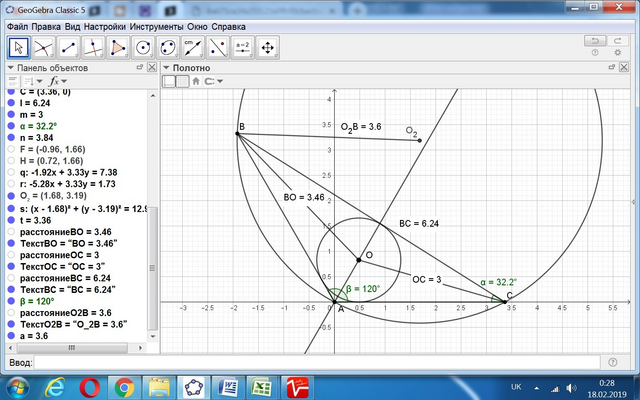
ВО и СО - это биссектрисы углов В и С соответственно.
Половина этих углов равна (180 - 120)/2 = 60/3 = 30°.
Отсюда угол ВОС равен 180 - 30 = 150°.
В треугольнике ВОС имеем 2 стороны и угол между ними.
Тогда ВС = √((2√3)² + 3² - 2*(2√3)*3*cos 150°) = √(12 + 6 - 12√3*(-√3/2)) = √(21 + 18) = √39.
Радиус описанной окружности треугольника АВС равен:
R = BC/(2sin120°) = √39/(2*(√3/2)) = √13 ≈ 3,6056 см.