Много баллов!!! Задание ** картинке.

Question

Много баллов!!! Задание на картинке.

---

Comments

а где угол 2?

Answer 1

1. насколько я понял, первый и второй углы вертикальные (второго угла нет на картинке), значит третий угол рсвен 180-(86:2)=180-43=137

2. биссектриса разбила угол АВС на 2, умножив 64 на 2 мы его и найдем (128). Угол DEB и АВС внутренние накрест лежащие углы, а значит угол DEB=180-128=52. Сумма углов треугольника равна 180 градусов, мы знаем два из них, поэтому можем узнать и третий 180-(DBE+DEB)=180-(64+52)=64(BDE)

Answer 2

1) ∠1 и ∠2 - накрест лежащие, значит ∠1 =∠2=86/2=43°

∠3 - смежный с ∠1, значит ∠3=180-∠1=180-43=137°

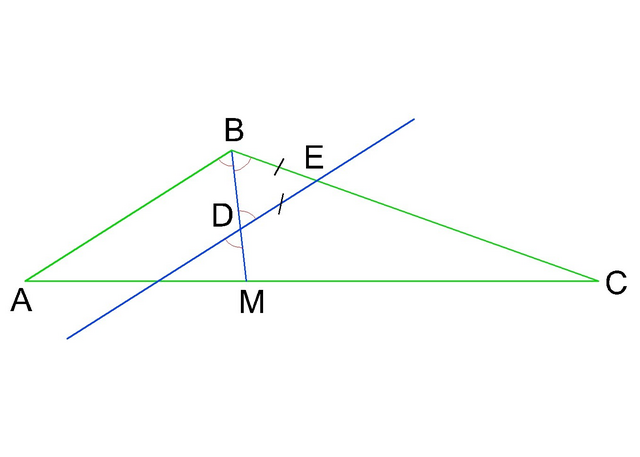
2) Рассмотрим рисунок.

АВ║ДЕ образуют с отрезком ВД накрест лежащие углы ∠АВД=∠ВДЕ, а так как ВМ-биссектриса ∠АВС, то ∠АВМ=∠АВД=∠ВДЕ=∠МВЕ=64°

Значит ΔВДЕ-равнобедренный, с двумя углами ∠ДВЕ=∠ЕДВ=64°.

Тогда из суммы углов треугольника ∠ВЕД=180-64*2=52°

Ответ:  ΔВДЕ имеет углы ∠ДВЕ=∠ЕДВ=64° и  ∠ВЕД=52°

---