Решением системы является точка пересечения графиков.
Построим каждый из них.

Построение:
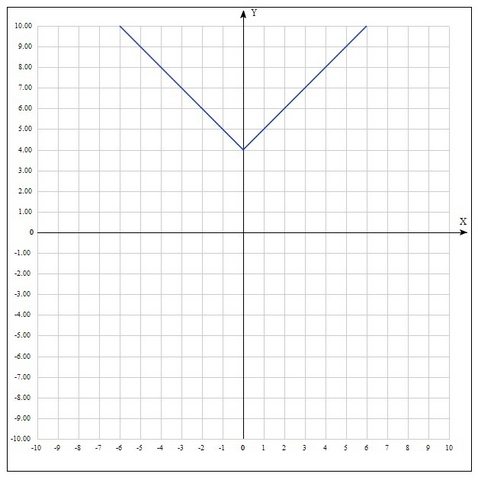
Шаг 1. Строим график  по точкам.
по точкам.

Шаг 2. Строим график  путём смещения графика
путём смещения графика  вверх на
вверх на  по
по 

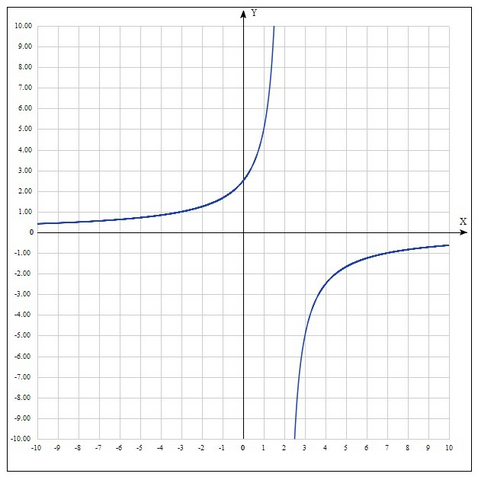
Дробно-линейная функция, график - гипербола.
Так как  ветви гиперболы находятся во второй и четвёртой четверти (относительно асимптот).
ветви гиперболы находятся во второй и четвёртой четверти (относительно асимптот).
Построение:
Шаг 1. Находим асимптоты графика.

Шаг 2. Строим график  по точкам, учитывая асимптоты.
по точкам, учитывая асимптоты.

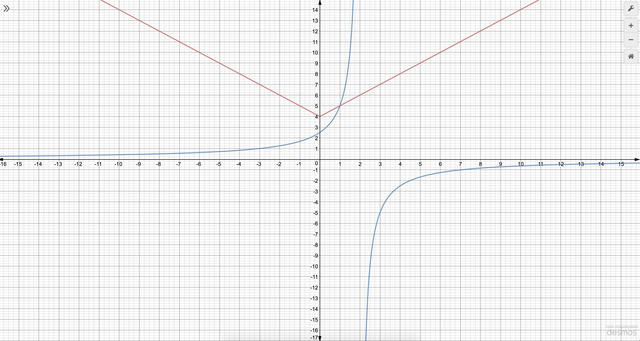
Решение данной системы:  - точка пересечения графиков.
- точка пересечения графиков.
Проверим, решив алгебраически.
 0} \atop {x+4=\frac{-5}{x-2};}} \right. } \atop {\left \{ {{x<0} \atop {-x+4=\frac{-5}{x-2};}} \right. }} \right. \Rightarrow \left \ [ {{\left \{ {{x>0} \atop {(x+4)(x-2)=-5;}} \right. } \atop {\left \{ {{x<0} \atop {(-x+4)(x-2)=-5};}} \right. }} \right. \Rightarrow_{x\neq2 } \\ \Rightarrow_{x\neq2 } \left \ [ {{\left \{ {{x>0} \atop {x^2+2x-3=0;}} \right. } \atop {\left \{ {{x<0} \atop {-x^2+6x-3=0}} \right. }} \right." alt="|x|+4=\frac{-5}{x-2};\\ \left \ [ {{\left \{ {{x>0} \atop {x+4=\frac{-5}{x-2};}} \right. } \atop {\left \{ {{x<0} \atop {-x+4=\frac{-5}{x-2};}} \right. }} \right. \Rightarrow \left \ [ {{\left \{ {{x>0} \atop {(x+4)(x-2)=-5;}} \right. } \atop {\left \{ {{x<0} \atop {(-x+4)(x-2)=-5};}} \right. }} \right. \Rightarrow_{x\neq2 } \\ \Rightarrow_{x\neq2 } \left \ [ {{\left \{ {{x>0} \atop {x^2+2x-3=0;}} \right. } \atop {\left \{ {{x<0} \atop {-x^2+6x-3=0}} \right. }} \right." align="absmiddle" class="latex-formula">
0} \atop {x+4=\frac{-5}{x-2};}} \right. } \atop {\left \{ {{x<0} \atop {-x+4=\frac{-5}{x-2};}} \right. }} \right. \Rightarrow \left \ [ {{\left \{ {{x>0} \atop {(x+4)(x-2)=-5;}} \right. } \atop {\left \{ {{x<0} \atop {(-x+4)(x-2)=-5};}} \right. }} \right. \Rightarrow_{x\neq2 } \\ \Rightarrow_{x\neq2 } \left \ [ {{\left \{ {{x>0} \atop {x^2+2x-3=0;}} \right. } \atop {\left \{ {{x<0} \atop {-x^2+6x-3=0}} \right. }} \right." alt="|x|+4=\frac{-5}{x-2};\\ \left \ [ {{\left \{ {{x>0} \atop {x+4=\frac{-5}{x-2};}} \right. } \atop {\left \{ {{x<0} \atop {-x+4=\frac{-5}{x-2};}} \right. }} \right. \Rightarrow \left \ [ {{\left \{ {{x>0} \atop {(x+4)(x-2)=-5;}} \right. } \atop {\left \{ {{x<0} \atop {(-x+4)(x-2)=-5};}} \right. }} \right. \Rightarrow_{x\neq2 } \\ \Rightarrow_{x\neq2 } \left \ [ {{\left \{ {{x>0} \atop {x^2+2x-3=0;}} \right. } \atop {\left \{ {{x<0} \atop {-x^2+6x-3=0}} \right. }} \right." align="absmiddle" class="latex-formula">
 0;\\ x_{1,2}=\frac{-b \pm \sqrt{D} }{2a} =\frac{-2 \pm \sqrt{16} }{2*1} = \left \ [ {{1} \atop {-3}} \right." alt="x^2+2x-3=0;\\ a=1,b=2,c=-3;\\ D=b^2-4ac=2^2-4*1*(-3)=16,>0;\\ x_{1,2}=\frac{-b \pm \sqrt{D} }{2a} =\frac{-2 \pm \sqrt{16} }{2*1} = \left \ [ {{1} \atop {-3}} \right." align="absmiddle" class="latex-formula">
0;\\ x_{1,2}=\frac{-b \pm \sqrt{D} }{2a} =\frac{-2 \pm \sqrt{16} }{2*1} = \left \ [ {{1} \atop {-3}} \right." alt="x^2+2x-3=0;\\ a=1,b=2,c=-3;\\ D=b^2-4ac=2^2-4*1*(-3)=16,>0;\\ x_{1,2}=\frac{-b \pm \sqrt{D} }{2a} =\frac{-2 \pm \sqrt{16} }{2*1} = \left \ [ {{1} \atop {-3}} \right." align="absmiddle" class="latex-formula">
 0\\ x_{1,2}=\frac{-b \pm \sqrt{D} }{2a} =\frac{-6 \pm \sqrt{24} }{2*(-1)}" alt="-x^2+6x-3=0;\\ a=-1,b=6,c=-3;\\ D=b^2-4ac=6^2-4*(-1)*(-3)=36-12=24,>0\\ x_{1,2}=\frac{-b \pm \sqrt{D} }{2a} =\frac{-6 \pm \sqrt{24} }{2*(-1)}" align="absmiddle" class="latex-formula">
0\\ x_{1,2}=\frac{-b \pm \sqrt{D} }{2a} =\frac{-6 \pm \sqrt{24} }{2*(-1)}" alt="-x^2+6x-3=0;\\ a=-1,b=6,c=-3;\\ D=b^2-4ac=6^2-4*(-1)*(-3)=36-12=24,>0\\ x_{1,2}=\frac{-b \pm \sqrt{D} }{2a} =\frac{-6 \pm \sqrt{24} }{2*(-1)}" align="absmiddle" class="latex-formula">
 0} \atop {\left \ [{{x_{1} =1;} \atop {x_{2} =-3}} \right. }} \right. } \atop {\left \{ {{x<0} \atop {\left \ [ {{x_{1} =\frac{-6+\sqrt{24} }{-2} } \atop {x_{2} =\frac{-6-\sqrt{24} }{-2}}} \right. }} \right. }} \right. \Rightarrow x=1" alt="\left \ [ {{\left \{ {{x>0} \atop {\left \ [{{x_{1} =1;} \atop {x_{2} =-3}} \right. }} \right. } \atop {\left \{ {{x<0} \atop {\left \ [ {{x_{1} =\frac{-6+\sqrt{24} }{-2} } \atop {x_{2} =\frac{-6-\sqrt{24} }{-2}}} \right. }} \right. }} \right. \Rightarrow x=1" align="absmiddle" class="latex-formula">
0} \atop {\left \ [{{x_{1} =1;} \atop {x_{2} =-3}} \right. }} \right. } \atop {\left \{ {{x<0} \atop {\left \ [ {{x_{1} =\frac{-6+\sqrt{24} }{-2} } \atop {x_{2} =\frac{-6-\sqrt{24} }{-2}}} \right. }} \right. }} \right. \Rightarrow x=1" alt="\left \ [ {{\left \{ {{x>0} \atop {\left \ [{{x_{1} =1;} \atop {x_{2} =-3}} \right. }} \right. } \atop {\left \{ {{x<0} \atop {\left \ [ {{x_{1} =\frac{-6+\sqrt{24} }{-2} } \atop {x_{2} =\frac{-6-\sqrt{24} }{-2}}} \right. }} \right. }} \right. \Rightarrow x=1" align="absmiddle" class="latex-formula">
Решено верно.
При построении графиков стоит учесть, что строить нужно оба графика на одной координатной плоскости.