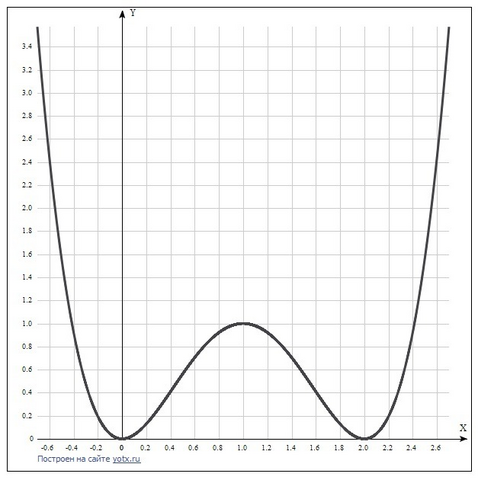
Дана функция у=х^2(x-2)^2.
1) Найти область определения. Выделить особые точки (точки разрыва). х ∈ (-∞; +∞).
2) Проверить наличие вертикальных асимптот в точках разрыва и на границах области определения. Нет.
3) Найти точки пересечения с осями координат.
С осью Оу: х = 0, у = 0.
С осью Ох: у = 0, х²(х - 2)² = 0.
х1 = 0, х - 2 = 0, х2 = 2.
4) Установить, является ли функция чётной или нечётной.
Так как переменная в квадратичных множителях - функция чётная.
5) Определить, является ли функция периодической или нет (только для тригонометрических функций). Не периодическая.
6) Найти точки экстремума и интервалы монотонности.
Производная равна: y' = 4x(x² - 3x + 2).
Приравняем нулю: 4x(x² - 3x + 2) = 0. х1 = 0.
x² - 3x + 2 = 0.
Ищем дискриминант: D=(-3)^2-4*1*2=9-4*2=9-8=1;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√1-(-3))/(2*1)=(1-(-3))/2=(1+3)/2=4/2=2;
x_2=(-√1-(-3))/(2*1)=(-1-(-3))/2=(-1+3)/2=2/2=1.
Имеем ещё 2 точки экстремума: х2 = 2 и х3 = 1.
Находим знаки производной на полученных промежутках:
х =-1 00,5 11,5 2 3
y' = -24 01,5 0-1,5 0 24
В точках х = 0 и х = 2 минимум функции, у = 0,
В точке х = 1 максимум функции, у = 1.
На промежутках (0; 1) и (2; +∞) функция возрастает.
На промежутках (-∞; 0) и (1; 2) функция убывает.
7) Найти точки перегиба и интервалы выпуклости-вогнутости.
Вторая производная функции равна: y'' = 4(3x² - 6x + 2).
Приравняем нулю множитель в скобках: 3x² - 6x + 2 = 0.
Ищем дискриминант: D=(-6)^2-4*3*2=36-4*3*2=36-12*2=36-24=12;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√12-(-6))/(2*3)=(√12+6)/(2*3)=(√12+6)/6=√12/6+6/6=(√3/3)+1 ≈ 1,57735;
x_2=(-√12-(-6))/(2*3)=(-√12+6)/(2*3)=(-√12+6)/6=-√12/6+6/6=(-√3/3)+1 ≈ 0,42265.
Находим знаки второй производной на полученных промежутках:
x = 0 0,42265 1 1,57735 2
y'' =8 0 -4 0 8
.
На промежутках (-∞; (-√3/3)+1)) и ((√3/3)+1); +∞) график вогнутый.
На промежутке ((-√3/3)+1); (√3/3)+1)) график выпуклый.
8) Найти наклонные асимптоты. Исследовать поведение на бесконечности. Асимптот нет.
9) Выбрать дополнительные точки и вычислить их координаты.
y(x)=x²(x−2)².
Таблица точек
xy
-0.62.43
-0.40.92
-0.20.19
00
0.20.13
0.40.41
0.60.71
0.80.92
1.01
1.20.92
1.40.71
1.60.41
1.80.13
2.00
2.20.19
2.40.92
2.62.43
10) Построить график и асимптоты. Дан в приложении.