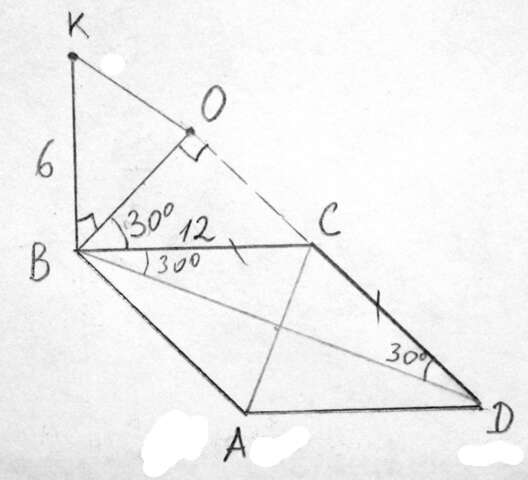
Назовем расстояние от точки К до прямой СД отрезком КО.
Тогда получаем прямоугольный ΔКВО с прямым ∠КВО, где известен катет ВК=6, а найти нужно гипотенузу КО.
Найдем второй катет ОВ. Он является проекцией отрезка КО на плоскость ромба и ОВ⊥ОД, а так как ОС лежит на прямой, образованной точками ОД, то и ОВ⊥ОС.
Рассмотрим треугольники ΔВДС, ΔВОД и ΔВОС .
ΔВДС - равнобедренный, с равными ∠ДВС=∠ВДС=∠В/2=30°.
ΔВОД - прямоугольный с исзвестными прямым ∠ВОД=90° и ∠ВДС=30°. Значит ∠ОВД=180-90-30=60°.
ΔВОС - прямоугольный с прямым ∠ВОС и известной гипотенузой ВС=12. Найдем ∠ОВС=∠ОВД-∠ДВС=60-30=30°. Найдем катет: ОВ=12·cos∠ОВС=12·cos 30°=6·√3
Рассмотрим наконец прямоугольный ΔКВО. Нам известны катеты КВ=6 и ОВ=6·√3. Найдем гипотенузу: КО=√(КВ²+ОВ²)=√(36+36·3)=√144=12
Ответ: расстояние от точки К до прямой СД равно 12 см.