Дано:
C₁ = 42 см - длина первой окружности
C₂ = 126 см длина второй
Найти: S=? - площадь кольца.
Пошаговое объяснение:
Длина окружности по формуле: C = 2π*R - прямо пропорциональна радиусу.
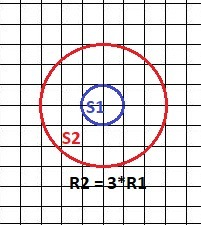
R₂/R₁ = 116/42 = 3 - радиус в 3 раза больше
S₁ =π*R₁² - площадь малой окружности.
Площадь окружности пропорциональна квадрату радиуса.
S₂ = π*R₂² = 9*S₁ - площадь в 9 раз больше
S = S₂ - S₁ = 8*S₁ - площадь кольца - искомое.
R₁ = C₁/(2*π) = 42 : (2*3.14) = 42 : 6.28 = 6.9878 ≈ 7 см - радиус малой окружности.
S₁ = π*R₁² = 3.14*7² 3,14*49 = 153,86 см² - площадь малой окружности.
S = 8*S₁ = 8*153.86 = 1230.88 см² - площадь кольца - ответ.
Или при π = 3.
1) R₁ = 42 : 6 = 7 см - радиус малой окружности.
2) S₁ = 3*7² = 3*49 = 147 см² - площадь малой окружности.
3) S = 8*S₁ = 8*147 = 1176 см² - площадь кольца - ответ.
Разница заметна - 54 см² - примерно 4,5%.