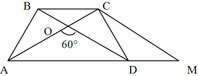
Пусть AD = a, BC = b, AC = a + b. Продолжим AD за точку D на расстояние DM = BC.
Тогда очевидно, что ?АСМ - равносторонний.
Но это значит, что угол АОD и угол ВОС - тоже равносторонние.
Отсюда непосредственно следует, что угол АОВ = угол СОD,
откуда имеем, что AB = CD.
Удачи! : )