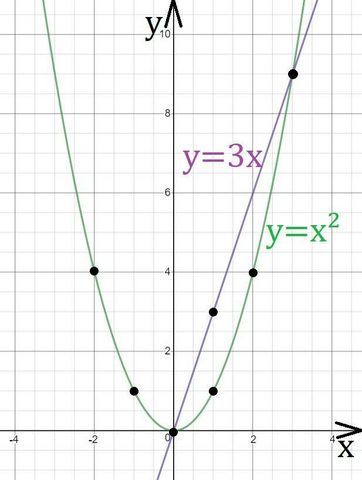
1.Розв'яжіть систему рівняння графічно. {y=x^2 {y=3x 2.Розв'яжіть рівняння методом...

Question

Дан 1 ответ

Правильный ответ

№1.

Прямую у=3х проведём через её две точки (0;0), (1;3).

Параболу у=х² построим по 5ти точкам, при этому (0;0) - вершина параболы. (-2;4), (-1;1), (1;1), (2;4).

По графикам видно, что общие точки (0;0), (3;9). Проверим это.

Точка (0;0) точно принадлежит обеим графикам, это уже считали.

9=3·3 и 9=3², поэтому точка (3;9) тоже является решением.

Ответ: (0;0) и (3;9).

№2.

$\displaystyle \left \{ {{x+y=5} \atop {x\cdot y=4}} \right.\quad \left \{ {{x=5-y\qquad } \atop {(5-y)y=4\; (1)}} \right. \\\\(1)\;y^2-5y+4=0;D=25-16=3^2\\\\\left[\begin{array}{ccc}y_1=\dfrac{5-3}2\\y_2=\dfrac{5+3}2\\\end{array} \quad \left[\begin{array}{ccc}y_1=1\\y_2=4\\\end{array}$

x₁ = 5-1 = 4

x₂ = 5-4 = 1

Ответ: (1;4) и (4;1).

№3.

Решим методом подстановки.

$\displaystyle \left \{ {{5+y=x^2} \atop {x^2+y^2=25}} \right. \quad \left \{ {{x^2=5+y\qquad \qquad } \atop {(5+y)+y^2=25\; (1)}} \right. \\\\(1)\; y^2+y-20=0;\; D=1+80=9^2\\\\\left[\begin{array}{ccc}y_1=\dfrac{-1-9}2\\y_2=\dfrac{-1+9}2\\\end{array} \quad \left[\begin{array}{ccc}y_1=-5\\y_2=4\\\end{array}$

x² = 5+y₁ = 5-5 = 0

x₁ = 0

x² = 5+y₂ = 5+4 = 3²

x₂₁ = -3

x₂₂ = 3

Ответ: (0;-5), (-3;4) и (3;4).

WhatYouNeed_zn (34.7k баллов) 28 Май, 20