1. Если ∠1 = ∠2, то а║в. Тогда ∠4=180-∠3=180-140=40°
2. а) ∠1=∠2=210/2=105°
∠3=180-∠2=180-105=75°
б) ∠3=х, тогда ∠1=∠2=180-х=х+40 ⇒ 2х=140 ⇒ х=70
Значит ∠3=70, ∠1=∠2=70+40=110°
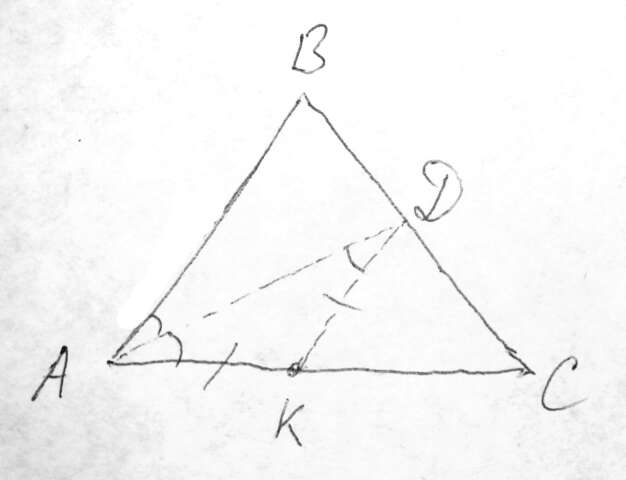
3. См. рис.
Т.к. АД - биссектриса ∠ВАС, то ∠ВАД=∠САД=35°
Т.к. АК=ДК, то, ΔАДК-равнобедренный, с равными углами ∠ДАК=∠АДК=35°
Тогда из суммы углов треугольника найдем ∠АКД=180-2·35=110°