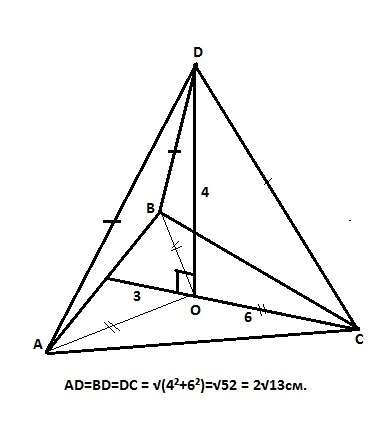
Точка D проецируется в центр описанной окружности, так как она равноудалена от вершин треугольника. В правильном треугольнике центры описанной и вписанной окружности совпадают и лежат на пересечении медиан треугольника, то есть делят медиану (высоту, биссектрису) в отношении 2:1, считая от вершины. Причем (1/3) медианы - это радиус вписанной окружности, а (2/3)медианы - радиус описанной окружности. В нашем случае (1/3) = 3 см. Тогда (2/3) = 6см. Из прямоугольного треугольника, образованного расстояниями от точки D до плоскости треугольника и радиусом описанной окружности (катеты) и расстоянием от точки D до вершин треугольника (гипотенуза) найдем искомое расстояние:
d = √(4²+6²)=√52 = 2√13см. Это ответ.