Ответ:
57 ед²
Пошаговое объяснение:
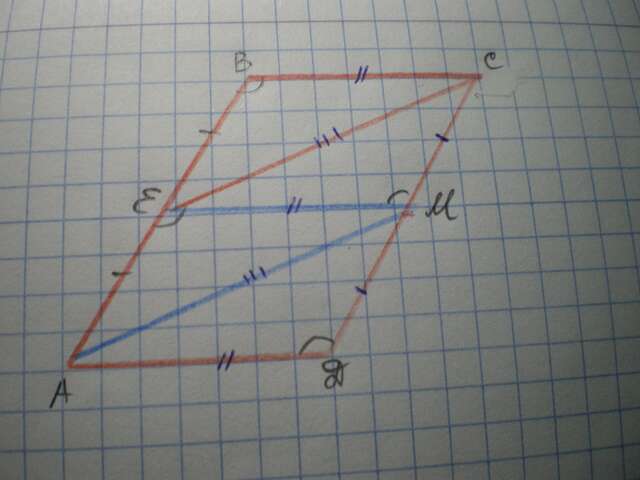
Дано: ABCD - параллелограмм, S=76 ед², АЕ=ВЕ. Найти S(DAEC).
Решение: проведем ЕМ║DA и АМ║ЕС.
Тогда ВСМЕ - параллелограмм, где СЕ - диагональ и делит его на 2 равных треугольника; DAEМ - параллелограмм, где АМ - диагональ и делит его на 2 равных треугольника.
∠В=∠ЕМС как противоположные углы параллелограмма ВСМЕ
∠D=∠АЕМ как противоположные углы параллелограмма АЕМD
∠AEM=∠EMC как внутренние накрест лежащие при АВ║СD и секущей ЕМ
значит, ΔВСЕ=ΔМЕС=ΔАЕМ=ΔDAМ.
Площадь этих треугольников в сумме равна S(АВСD)=76 ед², тогда
S(АЕСD)=3/4 S(АВСD) = 76:4*3=57 ед².