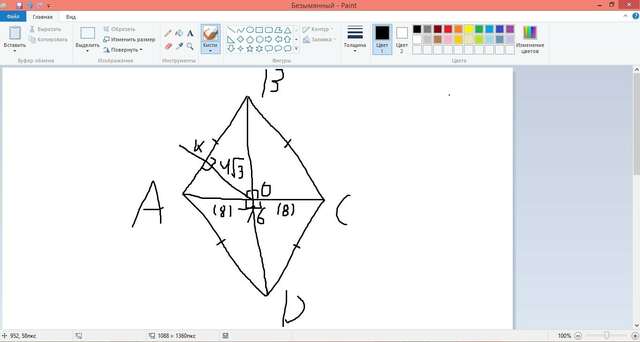
Ну,смотри, AO=OC по свойству п-грамма,а диагонали ромба взаимноперпендикулярнытоже по свойству самого ромба)),тогда можно применить формулу пропорциональных отрезков в прямоугольном треугольнике: OK^2=AO^2-AK^2(48=64-x),где x = 16.Так же по другой формуле можно найти KB: OK^2=AK*KB(48=16x),где x = 3,значит сторона ромба равна 19.Так же для этого треугольника можно применить теорему пифагора: AB^2(16+3=19)=AO^2+x^2(361=64+x),где x равен 297,а значит половина этой диагонали равно корень из 297 = 3 корень из 33,тогда вся диагональ равна 3 корень из 3 *2 = 6 корень из 33