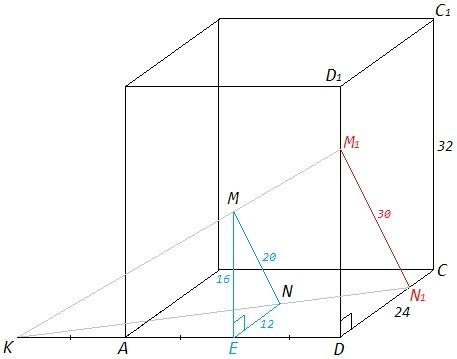
Проведем прямую KM в плоскости ADD1 до пересечения с ребром DD1 в точке M1.
Проведем прямую KN в плоскости ADC до пересечения с ребром DC в точке N1.
M1N1 - искомый отрезок.
E - середина AD.
EM - средняя линия в △DAD1, EM=DD1/2=16
EN - средняя линия в △DAC, EN=DC/2=12
Два угла с соответственно параллельными и одинаково направленными сторонами равны и лежат в параллельных плоскостях.
EM||DD1, EN||DC => ∠MEN=∠D1DC=90, (MEN)||(D1DC)
△MEN - египетский треугольник, множитель 4, MN=5*4=20
△EKM~△DKM1 (параллельные отсекают от угла подобные треугольники), EM/DM1 =EK/DK =2/3
Параллельные плоскости MEN и D1DC пересекаются плоскостью KMN, линии пересечения параллельны, MN||M1N1. В треугольниках MEN и M1DN1 стороны попарно параллельны, треугольники подобны.
△MEN~△M1DN1, MN/M1N1 =EM/DM1 =2/3 => M1N1=3/2 MN =30