№ 1.
AP⊥(ABC)(по условию)⇒BC⊥AP
BC⊥PD(по условию)
AP∩PD=P
BC⊥ двум пересекающимся прямым⇒BC⊥(PDA)⇒BC⊥любой прямой, лежащей в плоскости PDA⇒BC⊥AD,ч.т.д.
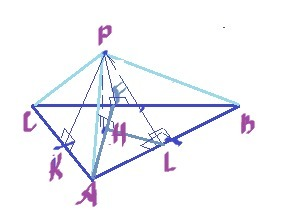
№ 2.
1)Найдём радиус описанной окружности треуг.ABC по т.Пифагора:
AH=√PA²-PH²
AH=√10²-8²=6
При этом заметим, что AH=BH=CH(как радиусы описанной окр.)
2)AF-медиана, биссектриса, высота в правильном треугольнике.
 (по св-ву медианы)
(по св-ву медианы)
Тогда AF=9.
3)HL-перпендикуляр к стороне AB(как радиус вписанной окружности)
При этом заметим, что HL=HK=HF(PH-общая сторона, а PL=PK=PF(по условию))
HL=HF=1/3AF(по св-ву медиан)⇒HL=3
4)по т.Пифагора:
AL=√AH²-HL²=√36-9=√27=3√3
5)2AL=AB=BC=AC=6√3
6)S=AF*BC*1/2=6√3*1/2*9=27√3