Найдите наименьшее значение первообразной функции y=2x+4, проходящей через точку (2;8).

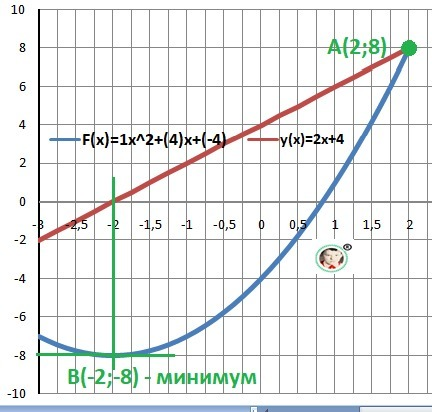
Ответ: Ymin(-2) = - 8

Пошаговое объяснение:

1) $Y(x)=\int\limits {(4+2x)} \, dx=\frac{4x}{1}+\frac{2x^2}{2}+C$

- первообразная полинома.

Важно: при такой записи интеграла - степень при Х увеличивается на 1 (единицу) и на эту новую степень дробь делится - мнемоника.

Находим значение С, при Х=2, У = 8

2) 2² + 4*2 + С = 8 - проходит через точку у=8 - решаем.

3) С = 8 - 4 - 78 = - 4 - нашли сдвиг и получили уравнение

4) F(x) = x² - 4*x - 4 = 0 - парабола и надо найти минимум - координату вершины. Преобразуем к полному квадрату по Х.

5) F(x) = (x²-4*x+4) - 4 -4 = (x-2)² - 8 - другая запись этого уравнения.

Думаем: Вершина параболы в точке А(-2,-8) и минимальное значение будет равно У = -8.

Рисунок к задаче в приложении.